前言
最近做项目(又)接触到了时间序列,任务是给一段序列,要求能检测出是否存在一个较为明显的周期性模式。
咨询了一下同行,主要利用快速傅立叶变换来进行频谱提取。在公司的数据上尝试了一下,效果还不错,在此总结一下思路。
本科的时候学习信号处理有接触过傅立叶变化,对时间域、频率域有一定了解。FFT算法的思想主要是基于频率域的信息。
基本思想
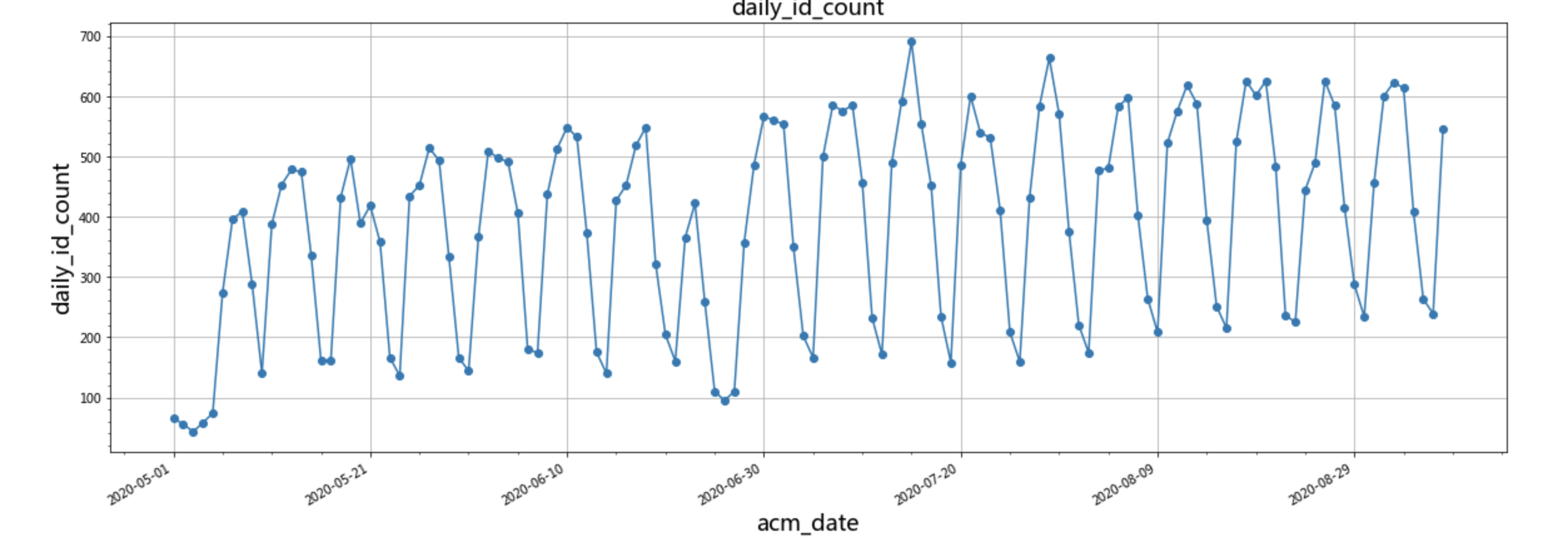
在原始波形上应用快速傅立叶变换(fft),每一个变换后的数值是一个复数,形式为a+bj,其中复数的模是对应的“振幅谱”,复数所对应的角度,即“相位谱”。
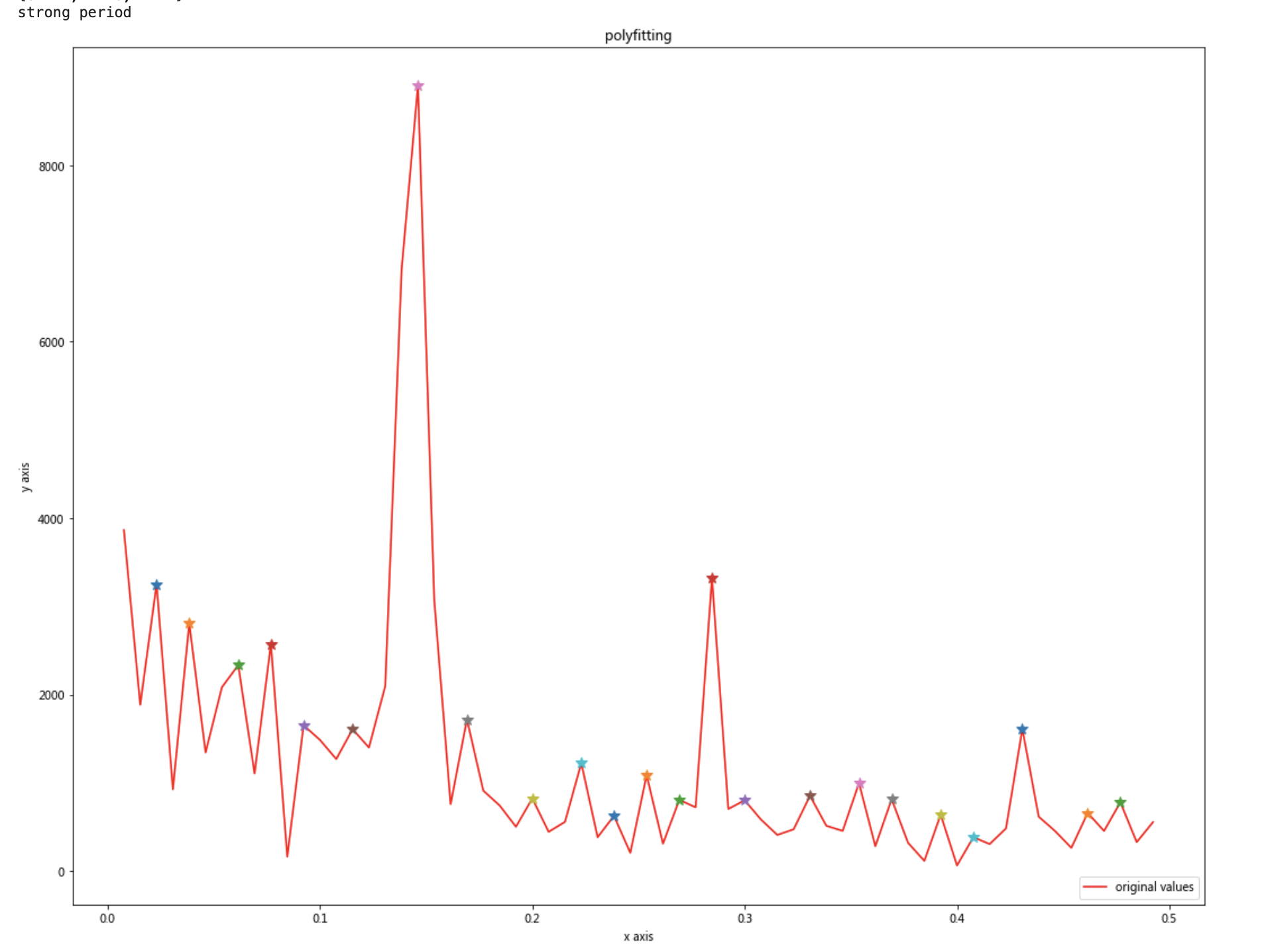
画出一段波形的振幅谱,可以直观地看出,哪个频率的信息量更大,信号更强。
对于一段没有噪声的周期性波形,它的振幅谱应当只有一个主频率,其对应的能量值也是最大的。
statsmodels
statsmodels的seasonal_decompose包,可以按照设定的周期,对一段时间序列进行季节性因素提取,得到的分别是趋势、周期、残差。
在做时间序列的预测问题时,可以利用分解后的数据进行多维度建模。
ts = df['value'] # ts: 时间序列
freq = 7 # freq: 周期
decomposition = seasonal_decompose(ts, period=freq, two_sided=False)
trend = decomposition.trend # 趋势
seasonal = decomposition.seasonal # 周期
residual = decomposition.resid # 残差
decomposition.plot()
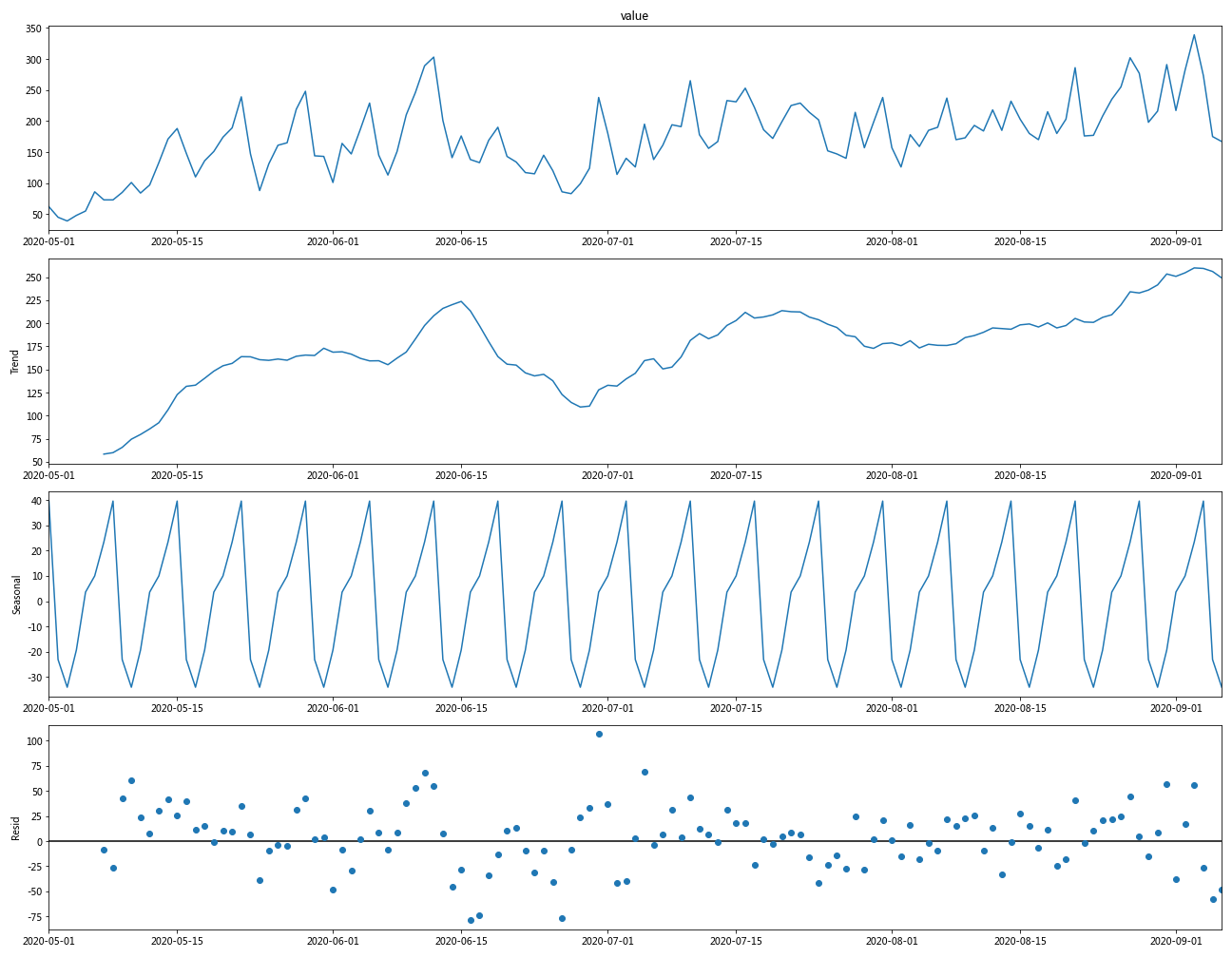
绘制FFT频谱图
def _fft_v1(x, y, _id, savefig=False, img_dir='tmp'):
"""
Given x and y, plot the fft results.
Return:
freqs: frequencies of input timeseries
pows: powers of each frequency
"""
import numpy.fft as fft
t = [i for i in range(len(x))]
S = y
complex_array = fft.fft(S)
# 得到分解波的频率序列
freqs = fft.fftfreq(len(t), t[1] - t[0])
# 复数的模为信号的振幅(能量大小)
pows = np.abs(complex_array)
检测每一个peak的位置和能量值,进行记录,用于之后进行周期性判断:
def _plot_fft_peak(freqs, pows, _id, savefig=False, img_dir='tmp'):
"""
Get all the peaks of the input fft results.
Return:
num_peak: a dict includes peaks information
_f: frequencies list
pows: powers list
"""
from scipy import signal
from scipy.signal import savgol_filter
_f = freqs[freqs > 0]
_p = pows[freqs > 0]
num_peak = signal.find_peaks(_p, distance=1) # distance表极大值点的距离至少大于等于的水平单位
return num_peak, _f, _p